How to Describe the Limit of a Function

Lim x x 0 f x L lim _ x to x_0 fx L x x 0 lim f x L. The limit of a rational function ie.

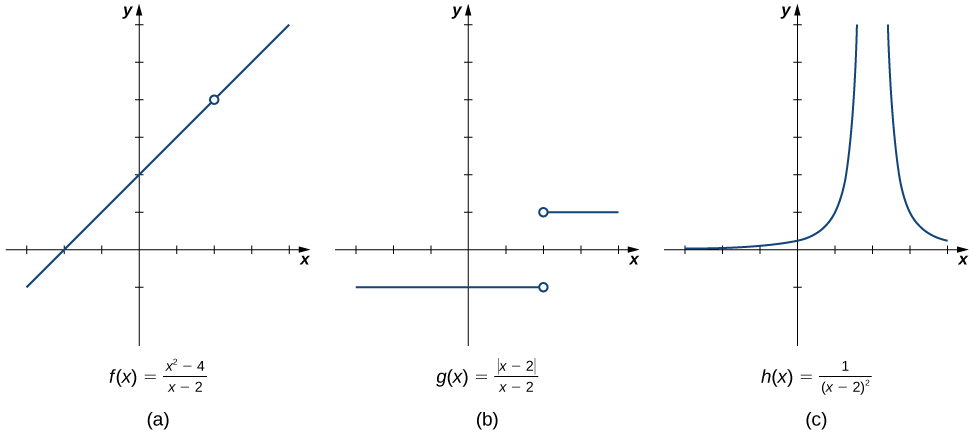
2 2 The Limit Of A Function Calculus Volume 1

If the limit of a function at a point does not exist it is still possible that the limits from the left and right at that point may exist.

. Let fleft x right be a function defined on an interval that contains x a except possibly at x a. LIM1B LO LIM1B1 EK Limits describe how a function behaves near a point instead of at that point. The limit of f x fx f x as x x x approaches x 0 x_0 x 0 is L L L ie.

Press Enter then grab the little square at the right hand corner of B2. If the limits of a function from the left and right exist and are equal then the limit of the function is that common value. If both one-sided limits exist and are equal then we say the limit exists.

The limit to be denoted by L is the unique real value that fx will approach as x approaches c. Formal Definition of a Function Limit. For any polynomial function P x and for and real number a we can find the limit as x approaches a by substitution.

The behavior of a function fxas x increases without bound or decreases without bound is sometimes called theend behavior of the function. If your limit involves trigonometric terms such as sine or cosine try to replace parts of the function with alternative forms of the terms if direct substitution gives you an indeterminate form. In symbols we write the process as lim fx L x c This is read The limit of fx as x approaches c is L Consider lim 1 3x x 2 First consider approaching.

Use a graph to estimate the limit of a function or to identify when the limit does not exist. What is meant by an indeterminate form. Suppose fx is defined when x is near the number a.

The limit of a polynomial function as is obtained by replacing by in the polynomial and then evaluating the required limit. If the limits of a function from the left and right exist and are equal then the limit of the function is that common value. Informally a function f assigns an output fx to every input x.

2 2 x 2 x 1 4 lim t 5. Is used to describe one sided. LIMITS The most basic use of limits is to describe how a function behaves as the independent variable approaches a given value.

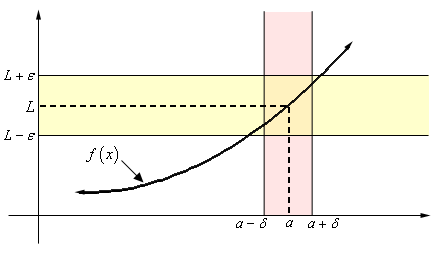
The limit of the function fx at the point a is L if and only if for any epsilon 0 there exists delta 0 such that if 0 x - a delta then fx - L. In mathematics the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input. Use a table of values to estimate the limit of a function or to identify when the limit does not exist.

Define one-sided limits and provide examples. We start with the function. The quotient of two polynomials on.

If the function is defined at a then the limit is just fa but the limit might also exist if the function is not defined in a. Use a table of values to estimate the limit of a function or to identify when the limit does not exist. LIMITS AT INFINITY AND HORIZONTALASYMPTOTES If the values of a variable x increase without bound then we write x and if the values of x decrease without bound then we write x.

In this notation we will note that we always give the function that were working with and we also give the value of x x or t t that we are moving in towards. The limit notation for the two problems from the last section is lim x1 22x2 x 1 4 lim t5 t36t225 t 5 15 lim x 1. Then we say that mathop lim limits_x to a fleft x right L if for every number varepsilon 0 there is some number delta 0 such that.

Type the numbers 1 through 10 in column A of a worksheet. The formal definition of limits is. How do you find a limit of a function with an indeterminate form.

To understand what limits are lets look at an example. Describe how to find the limit of a polynomial function px as x approaches c. When youre given a complex rational function you use the fourth and final algebraic limit-finding technique.

First method to try when finding the limit of a function. Using correct notation describe the limit of a function. Formal definitions first devised in the early 19th century are given below.

Every polynomial function with real coefficients has from. If for every ϵ 0 epsilon 0 ϵ 0 there exists δ 0 delta 0 δ 0 such that for all x x x. P x anxn an1xn1 a1x a0.

Limits describe the behavior of a function if you look at a region around a certain number. This means that f is defined on some open interval that contains a except possibly at a itself. We say that the function has a limit L at an input p if fx gets closer and closer to L as.

We may use limits to describe infinite behavior of a function at a point. This problem has been solved. The x 13 terms cancel leaving you with this result.

Where the ai are real numbers and n is a nonnegative integer. If the limit of a function at a point does not exist it is still possible that the limits from the left and right at that point may exist. Use a graph to estimate the limit of a function or to identify when the limit does not exist.

Drag this square to the bottom of column B2. For example let us examine the behavior of the function for x-values closer and closer to 2. The limit inferior is the smallest.

Using correct notation describe the limit of a function. Lim x-0 sinxx 1. When you get to the n click on cell A1.

Lets determine the limits of the function when tens to or. We may use limits to describe infinite behavior of a function at a point. Is the limit of the quotient the terms of the highest degree of the two polynomials on.

Type the formula in cell B2. For example if your function is fx 1 - cos²xsinx you could replace 1 - cos²x with sin²x as sin²x cos²x 1 and then cancel the sinx in the denominator leaving you. When you plug 13 into the function you get 16 which is the limit.

This simple yet powerful idea is the basis of all of calculus. T 3 6 t 2 25 t 5 15. 1 x x x f 2.

That is lim xa P x P a. See the answer See the. Find the limit by finding the lowest common denominator.

Intuitive Definition of a Limit. The proof uses the properties of limits.

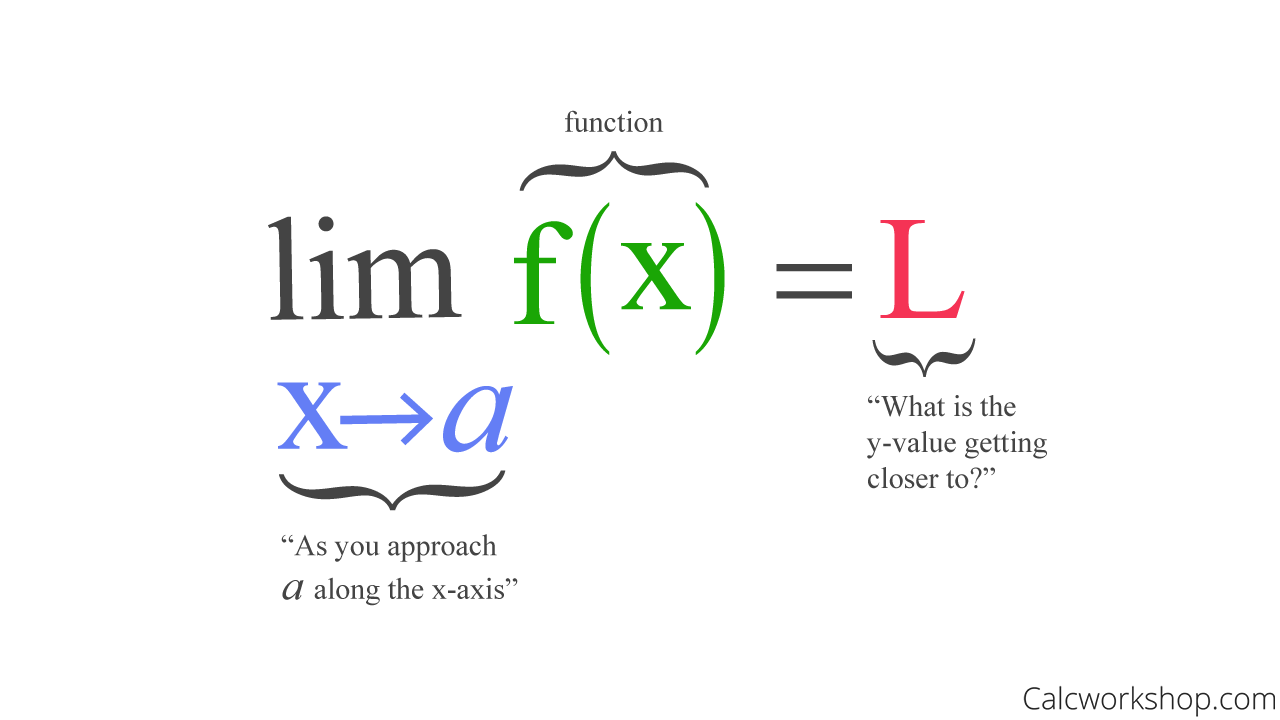
Finding Limits Graphically How To W 29 Examples

10 Flamingo Math Limits Worksheet Ap Calculus Ap Calculus Ab Calculus Teacher

An Extensive Explanation About The Epsilon Delta Definition Of Limits Calculus Studying Math Definitions

Calculus Finding Limits Analytically Maze Plus Hw Math Lesson Plans Calculus Ap Calculus

How To Find The Limit Using Squeeze Theorem Ap Calculus Theorems Calculus

Limits On A Graph Math Blog Math Calculus

Pin On Calculus Lesson Ideas

Calculus I The Definition Of The Limit

Calculus I The Limit

Oracle Database 12c Sql Fundamentals 1z0 061 Certification Exam Topics Album On Imgur Oracle Database Sql Exam

Derivatives Flashcards Flashcards Calculus Free Math Resources

Calculating Limit Simor Ap Calculus Math Methods Mathematics Worksheets

Ap Calculus Back To School Weekly Review 2 Made By Teachers In 2021 Ap Calculus Calculus Simplifying Rational Expressions

2 2 The Limit Of A Function Calculus Volume 1

Limit Laws Utrgv

Limits Day 5 Of A Jet Tour Of Calculus Calculus Ap Calculus Rational Function

Limit Is A Very Old Concept In The Mathematics And When We Talk About Calculus Without Limit We Can T Put Any Step Calculus Mathematics Left And Right Handed

Limits Formula Meaning Examples

Calculus Limits Of Functions Video Lessons Examples Solutions